Home
Size, Strength and Length

It is often implied that because big men aren't as strong relative to their size compared to smaller men, that the big man is somehow not realising his potential or perhaps he is not really trying hard enough.
The reality is that big men have more bulk per unit of area than a small man. In effect not only do they have to move their bigger bulks but they have proportionately less muscle cross sectional areas to generate force.
It works like this;
 A
A
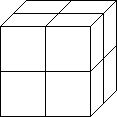 B
B
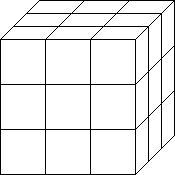 C
C
-
Cube B's linear dimensions are 2 times that of A, but its surface area is 4 times greater and its volume is 8 times greater.
-
Cube C's linear dimensions are 3 times that of A, but its surface area is 9 times greater and its volume is 27 times greater.
You don't need a calculator to figure this you can see that it is so from the diagrams. Thus the volume goes up faster than the area and area goes up faster than the lengths as the cube gets bigger.
The area goes up by the square of the linear dimensions and the volume goes up by the cube of the linear dimensions. These rules apply to any shape (think of all shapes as being made of tiny cubes), in effect you might consider living bodies to be made up of cubular cells or cubular atoms for that matter.
Formulas
Using the square and cube rules mention earlier, the following relationships between the variables L, S and M apply:
L2 ∝ S
L3 ∝ M
S ∝ M2/3
M ∝ S3/2
L - length (height)
S - area (strength)
M - volume (mass)
∝ - proportional to
These rules assume that the mass of an object is proportional to its volume and that the strength of an object is proportional to its (cross-sectional) area.
Example
I am 175 cm tall and my armwrestling buddy Steve is 185 cm;
Strength (185/175)2 = 1.0572 = 1.118
Mass (185/175)3 = 1.0573 = 1.181
Thus Steve is 1.057 times taller than me and if he were the same shape as me he would be 1.181 time heavier and the cross sectional area of his muscles would be 1.118 times greater than mine.
Thus if I weigh 75 kg, Steve would weigh;
1.181 × 75 = 88.6 kg
However, Steve actually weights about 105 kg, so he is more spherical than me. This would mean that his muscle cross-sectional areas would be greater than the expected 1.118 times;
Strength 105/88.6 = 1.19
1.19 × 1.118 = 1.33
Steve's arm is actually about 17.5" whereas mine is a mere 13";
Strength (17.5/13)2 = 1.3462 = 1.812
Thus from his height his strength would be 11.8% greater than mine, but from his mass he would be 33% stronger and from his arm size he would be 81.2% stronger. Actual tests shows that his table curling strength against springs and dumbbells is about 25-30% stronger, which suggest that my arm curling strength per unit cross section of muscle is stronger than Steve's (in absolute terms Steve is obviously stronger). I'm ignoring Steve's greater fatness in these calculations.
Ants
These rules explain why it is that bigger animals have thicker limbs or conversely why small particles float in air whilst a large lump of the same density doesn't.
Consider the oft stated fact that insects are very strong in proportion to their weight. An insect that weighs 0.1 g compared to a 100 kg man is obviously 1/1000000th the weight of the man, but from the formulas is only 1/10000th of his strength. The insect is therefore 100 times stronger in proportion to its weight compared to a man. Obviously an insect is not the same shape as a man, its legs are relatively skinny because it has such an abundance of superstrength it can afford to lose some of its 100 advantage - the ant also doesn't have to lug around it tiny mass, a mass which is very small in proportion to its size compared to a man (an ant would feel like a 100 kg man weighing 1 kg).
Tallness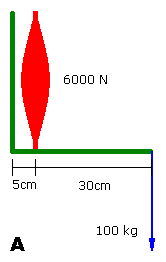
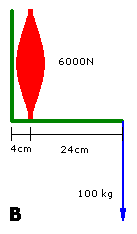
Occasionally a lifter will whine that he is 'tall'. Tall seems to be anything 6' or above whereas anything under 6' is suddenly short.
The implication by the tall person is that he has long limbs and thus any resistance will impose a long leverage. This is, of course, true - however it is also true that his muscles will have an equally long leverage which thus cancels out this leverage 'disadvantage'.
Look at the diagrams; assume the tall person (A) has forearms 35 cm long and is 1.92 m tall; the short person (B) has 28 cm forearms and is 1.6 m tall. A is thus 25% taller than B.
Both individuals have the same size muscle cross sections and therefore the same circumference upper arms. Thus in this example their biceps generates 6000 N of force, so they can both support 100 kg in a barbell curl. This is because in each case the barbell's lever arm is 6 times greater than the muscle's lever arm.
In short all that has to be done is to take the circumference measurement of a person's limb to indicate potential strength.
Acceleration
However when it comes to moving a limb through the same angular distance then a tall person will have to generate more force. For example if A and B's muscles both contract in the same time period (t) then A will have to move through 25% more distance (s) and so create 25% more acceleration (s/t2) force as B.
Of course there is nothing to say that a taller man must lift the weight in the same time period. For example a tall Olympic weightlifter may have to lift the weight further but this gives him more distance in which to build up speed.
Torque
Tall people also have an advantage in that because their muscle lever arm is proportionately greater they develop proportionately greater torque.
For example A develops 3000 N of force at 10 cm from the elbow joint, whereas B develops 2400 N at 10 cm. This is advantageous when picking up bulky objects for example an atlas stone. Similarly wrestlers could headlock somebody and throw them more easily. In both cases the effect of being taller is that when picking up a bulky object the object is effectively closer to the joints of a tall person so he can generate greater force.
Conclusion
A tall person has more room for bigger muscles to develop, his resistance lever arm is longer but this is cancelled by his greater muscle lever arm, he can generate greater velocities and greater torques. The amount a big person lifts in proportion to bodyweight should follow the formula S ∝ M2/3 not S ∝ M (bodyweight lifted must also be taken into account) so he is weaker in proportion to bodyweight and is also heavier in proportion to his height.
27th September 2023